Алгоритм деления «уголком» многочленов от одной переменной. Деление натуральных чисел столбиком, примеры, решения
Деление натуральных чисел, особенно многозначных, удобно проводить особым методом, который получил название деление столбиком (в столбик) . Также можно встретить название деление уголком . Сразу отметим, что столбиком можно проводить как деление натуральных чисел без остатка , так и деление натуральных чисел с остатком .
В этой статье мы разберемся, как выполняется деление столбиком. Здесь мы поговорим и о правилах записи, и о всех промежуточных вычислениях. Сначала остановимся на делении столбиком многозначного натурального числа на однозначное число. После этого остановимся на случаях, когда и делимое и делитель являются многозначным натуральными числами. Вся теория этой статьи снабжена характерными примерами деления столбиком натуральных чисел с подробными пояснениями хода решения и иллюстрациями.
Навигация по странице.
Правила записи при делении столбиком
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида . Например, если делимым является число 6 105
, а делителем – 5
5, то их правильная запись при делении в столбик будет такой:
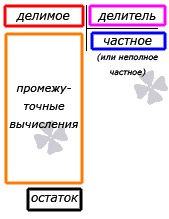
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком.

Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места. Например, при делении столбиком натурального числа 614 808
на 51 234
(614 808
– шестизначное число, 51 234
– пятизначное число, разница в количестве знаков в записях равна 6−5=1
) для промежуточных вычислений потребуется меньше места, чем при делении чисел 8 058
и 4
(здесь разница в количестве знаков равна 4−1=3
). Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:
Теперь можно переходить непосредственно к процессу деления натуральных чисел столбиком.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком
Понятно, что разделить одно однозначное натуральное число на другое достаточно просто, и делить эти числа в столбик нет причин. Однако будет полезно отработать начальные навыки деления столбиком на этих простых примерах.
Пример.
Пусть нам нужно разделить столбиком 8 на 2 .
Решение.
Конечно, мы можем выполнить деление при помощи таблицы умножения , и сразу записать ответ 8:2=4 .
Но нас интересует, как выполнить деление этих чисел столбиком.
Сначала записываем делимое 8
и делитель 2
так, как того требует метод:
Теперь мы начинаем выяснять, сколько раз делитель содержится в делимом. Для этого мы последовательно умножаем делитель на числа 0 , 1 , 2 , 3 , … до того момента, пока в результате не получим число, равное делимому, (либо число большее, чем делимое, если имеет место деление с остатком). Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.
Поехали: 2·0=0
; 2·1=2
; 2·2=4
; 2·3=6
; 2·4=8
. Мы получили число, равное делимому, поэтому записываем его под делимым, а на место частного записываем число 4
. При этом запись примет следующий вид:
Остался завершающий этап деления однозначных натуральных чисел столбиком. Под числом, записанным под делимым, нужно провести горизонтальную черту, и провести вычитание чисел над этой чертой так, как это делается при вычитании натуральных чисел столбиком . Число, получающееся после вычитания, будет остатком от деления. Если оно равно нулю, то исходные числа разделились без остатка.
В нашем примере получаем
Теперь перед нами законченная запись деления столбиком числа 8 на 2 . Мы видим, что частное 8:2 равно 4 (и остаток равен 0 ).
Ответ:
8:2=4 .
Теперь рассмотрим, как осуществляется деление столбиком однозначных натуральных чисел с остатком.
Пример.
Разделим столбиком 7 на 3 .
Решение.
На начальном этапе запись выглядит так:
Начинаем выяснять, сколько раз в делимом содержится делитель. Будем умножать 3
на 0
, 1
, 2
, 3
и т.д. до того момента, пока не получим число равное или большее, чем делимое 7
. Получаем 3·0=0<7
; 3·1=3<7
; 3·2=6<7
; 3·3=9>7
(при необходимости обращайтесь к статье сравнение натуральных чисел). Под делимым записываем число 6
(оно получено на предпоследнем шаге), а на место неполного частного записываем число 2
(на него проводилось умножение на предпоследнем шаге).
Осталось провести вычитание, и деление столбиком однозначных натуральных чисел 7
и 3
будет завершено.
Таким образом, неполное частное равно 2 , и остаток равен 1 .
Ответ:
7:3=2 (ост. 1) .
Теперь можно переходить к делению столбиком многозначных натуральных чисел на однозначные натуральные числа.
Сейчас мы разберем алгоритм деления столбиком . На каждом его этапе мы будем приводить результаты, получающиеся при делении многозначного натурального числа 140 288 на однозначное натуральное число 4 . Этот пример выбран не случайно, так как при его решении мы столкнемся со всеми возможными нюансами, сможем подробно разобрать их.
Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
Первой слева цифрой в записи делимого 140 288
является цифра 1
. Число 1
меньше, чем делитель 4
, поэтому смотрим еще и на следующую слева цифру в записи делимого. При этом видим число 14
, с которым нам и предстоит работать дальше. Выделяем это число в записи делимого.
Следующие пункты со второго по четвертый повторяются циклически, пока деление натуральных чисел столбиком не будет завершено.
Сейчас нам нужно определить, сколько раз делитель содержится в числе, с которым мы работаем (для удобства обозначим это число как x ). Для этого последовательно умножаем делитель на 0 , 1 , 2 , 3 , … до того момента, пока не получим число x или число больше, чем x . Когда получается число x , то мы записываем его под выделенным числом по правилам записи, используемым при вычитании столбиком натуральных чисел. Число, на которое проводилось умножение, записывается на место частного при первом проходе алгоритма (при последующих проходах 2-4 пунктов алгоритма это число записывается правее уже находящихся там чисел). Когда получается число, которое больше числа x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место частного (или правее уже находящихся там чисел) записываем число, на которое проводилось умножение на предпоследнем шаге. (Аналогичные действия мы проводили в двух примерах, разобранных выше).
Умножаем делитель 4
на числа 0
, 1
, 2
, …, пока не получим число, которое равно 14
или больше 14
. Имеем 4·0=0<14
, 4·1=4<14
, 4·2=8<14
, 4·3=12<14
, 4·4=16>14
. Так как на последнем шаге мы получили число 16
, которое больше, чем 14
, то под выделенным числом записываем число 12
, которое получилось на предпоследнем шаге, а на место частного записываем число 3
, так как в предпоследнем пункте умножение проводилось именно на него.
На этом этапе из выделенного числа вычитаем столбиком число, расположенное под ним. Под горизонтальной линией записывается результат вычитания. Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком). Здесь же для своего контроля не лишним будет сравнить результат вычитания с делителем и убедиться, что он меньше делителя. В противном случае где-то была допущена ошибка.
Нам нужно вычесть столбиком из числа 14
число 12
(для корректности записи нужно не забыть поставить знак «минус» слева от вычитаемых чисел). После завершения этого действия под горизонтальной чертой оказалось число 2
. Теперь проверяем свои вычисления, сравнивая полученное число с делителем. Так как число 2
меньше делителя 4
, то можно спокойно переходить к следующему пункту.
Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается. После этого выделяем число, образовавшееся под горизонтальной чертой, принимаем его в качестве рабочего числа, и повторяем с ним со 2 по 4 пункты алгоритма.
Под горизонтальной чертой справа от уже имеющейся там цифры 2
записываем цифру 0
, так как именно цифра 0
находится в записи делимого 140 288
в этом столбце. Таким образом, под горизонтальной чертой образуется число 20
.
Это число 20
мы выделяем, принимаем в качестве рабочего числа, и повторяем с ним действия второго, третьего и четвертого пунктов алгоритма.
Умножаем делитель 4
на 0
, 1
, 2
, …, пока не получим число 20
или число, которое больше, чем 20
. Имеем 4·0=0<20
, 4·1=4<20
, 4·2=8<20
, 4·3=12<20
, 4·4=16<20
, 4·5=20
. Так как мы получили число, равное числу 20
, то записываем его под отмеченным числом, а на месте частного, справа от уже имеющегося там числа 3
записываем число 5
(на него производилось умножение).
Проводим вычитание столбиком. Так как мы вычитаем равные натуральные числа, то в силу свойства вычитания равных натуральных чисел в результате получаем нуль. Нуль мы не записываем (так как это еще не завершающий этап деления столбиком), но запоминаем место, на котором мы его могли записать (для удобства это место мы отметим черным прямоугольником).
Под горизонтальной линией справа от запомненного места записываем цифру 2
, так как именно она находится в записи делимого 140 288
в этом столбце. Таким образом, под горизонтальной чертой мы имеем число 2
.
Число 2
принимаем за рабочее число, отмечаем его, и нам еще раз придется выполнить действия из 2-4
пунктов алгоритма.
Умножаем делитель на 0
, 1
, 2
и так далее, и сравниваем получающиеся числа с отмеченным числом 2
. Имеем 4·0=0<2
, 4·1=4>2
. Следовательно, под отмеченным числом записываем число 0
(оно было получено на предпоследнем шаге), а на месте частного справа от уже имеющегося там числа записываем число 0
(на 0
мы проводили умножение на предпоследнем шаге).
Выполняем вычитание столбиком, получаем число 2
под горизонтальной чертой. Проверяем себя, сравнивая полученное число с делителем 4
. Так как 2<4
, то можно спокойно двигаться дальше.
Под горизонтально чертой справа от числа 2 дописываем цифру 8
(так как она находится в этом столбце в записи делимого 140 288
). Таким образом, под горизонтальной линией оказывается число 28
.
Принимаем это число в качестве рабочего, отмечаем его, и повторяем действия 2-4
пунктов.
Здесь никаких проблем возникнуть не должно, если Вы были внимательны до настоящего момента. Проделав все необходимые действия, получается следующий результат.
Осталось последний раз провести действия из пунктов 2
, 3
, 4
(предоставляем это Вам), после чего получится законченная картина деления натуральных чисел 140 288
и 4
в столбик:
Обратите внимание, что в самой нижней строчке записано число 0 . Если бы это был не последний шаг деления столбиком (то есть, если бы в записи делимого в столбцах справа оставались цифры), то этот нуль мы бы не записывали.
Таким образом, посмотрев на законченную запись деления многозначного натурального числа 140 288 на однозначное натуральное число 4 , мы видим, что частным является число 35 072 , (а остаток от деления равен нулю, он находится в самой нижней строке).
Конечно же, при делении натуральных чисел столбиком Вы не будете настолько подробно описывать все свои действия. Ваши решения будут выглядеть примерно так, как в следующих примерах.
2 по 4 этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.
На первом этапе деления в столбик многозначных натуральных чисел нужно смотреть не на первую слева цифру в записи делимого, а на такое их количество, сколько знаков содержится в записи делителя. Если число, определяемое этими цифрами, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого. После этого выполняются действия, указанные во 2 , 3 и 4 пункте алгоритма до получения конечного результата.
Осталось лишь посмотреть применение алгоритма деления столбиком многозначных натуральных чисел на практике при решении примеров.
Пример.
Выполним деление столбиком многозначных натуральных чисел 5 562 и 206 .
Решение.
Так как в записи делителя 206
участвуют 3
знака, то смотрим на первые 3
цифры слева в записи делимого 5 562
. Эти цифры соответствуют числу 556
. Так как 556
больше, чем делитель 206
, то число 556
принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.
Теперь умножаем делитель 206
на числа 0
, 1
, 2
, 3
, … до того момента, пока не получим число, которое либо равно 556
, либо больше, чем 556
. Имеем (если умножение выполняется сложно, то лучше выполнять умножение натуральных чисел столбиком): 206·0=0<556
, 206·1=206<556
, 206·2=412<556
, 206·3=618>556
. Так как мы получили число, которое больше числа 556
, то под выделенным числом записываем число 412
(оно было получено на предпоследнем шаге), а на место частного записываем число 2
(так как на него проводилось умножение на предпоследнем шаге). Запись деления столбиком принимает следующий вид:
Выполняем вычитание столбиком. Получаем разность 144
, это число меньше делителя, поэтому можно спокойно продолжать выполнение требуемых действий.
Под горизонтальной линией справа от имеющегося там числа записываем цифру 2
, так как она находится в записи делимого 5 562
в этом столбце:
Теперь мы работаем с числом 1 442
, выделяем его, и проходим пункты со второго по четвертый еще раз.
Умножаем делитель 206
на 0
, 1
, 2
, 3
, … до получения числа 1 442
или числа, которое больше, чем 1 442
. Поехали: 206·0=0<1 442
, 206·1=206<1 442
, 206·2=412<1 332
, 206·3=618<1 442
, 206·4=824<1 442
, 206·5=1 030<1 442
, 206·6=1 236<1 442
, 206·7=1 442
. Таким образом, под отмеченным числом записываем 1 442
, а на месте частного правее уже имеющегося там числа записываем 7
:
Проводим вычитание столбиком, получаем нуль, но сразу его не записываем, а лишь запоминаем его позицию, потому что не знаем, завершается ли на этом деление, или придется еще раз повторять шаги алгоритма:
7 002
, и остаток от деления равен 11
.
Ответ:
238 079:34=7 002 (ост. 11) .
Список литературы.
- Математика. Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
- Математика. Любые учебники для 5 классов общеобразовательных учреждений.
Когда речь идет о технике деления чисел, то этот процесс рассматривают как действие деления с остатком: разделить целое неотрицательное число а на натуральное число b - это значит найти такие целые неотрицательные числа q r, что а = bq + r, причем 0 £ r < b.
Выясним сначала, как осуществляется деление на однозначное число . Если на однозначное число делят однозначное или двузначное (не превышающее 89), то используется таблица умножения однозначных чисел. Например , частным чисел 54 и 9 будет число 6, так как 9 × 6 = 54. Если же надо разделить 51 на 9, то находят ближайшее к нему меньшее число, которое делится на 9 - это число 45, и, следовательно, неполным частным при делении 51 на 9 будет число 5. Чтобы найти остаток, надо из 51 вычесть 45: 51 - 45 = 6. Таким образом, 51 = 9×5 + 6, т.е. при делении 51 на 9 получается неполное частное 5 и остаток, равный 6. Записать это можно иначе, при помощи деления уголком:
Будем теперь делить трехзначное число на однозначное, например, 378 на 4. Разделить 378 на 4 - это значит найти такое неполное частное q и остаток r , что 378 = 4 q + r , причем остаток r должен удовлетвори условию 0 £ r < b , а неполное частное q - условию 4 q £ 378 < 4(q + 1).
Определим, сколько цифр будет содержаться в записи числа q. Однозначным число q быть не может, так как тогда произведение 4 q может быть максимально равно 36 и, значит, не будут выполняться условий сформулированные выше для r и q . Если число q двузначное, т.е. есть 10 < q < 100, то тогда 40 < 4 q < 400 и, следовательно, 40 < 378 < 400, что верно. Значит, частное чисел 378 и 4 - число двузначное.
Чтобы найти цифру десятков частного, умножим последовательно делитель 4 на 20, 30, 40 и т.д. Поскольку 4 × 90 = 360, а 4 × 100 = 400, и 360 < 378 < 400, то неполное частное заключено между числами90 и100, т.е. q = 90 + q 0. Но тогда должны выполняться неравенства: 4× (90 + q 0) £ 378 < 4 × (90 q + q 0 + 1), откуда 360 + 4 q 0 £ 378 < 360 + 4(q 0 + 1) и 4 q 0 £ 18 < 4(q 0 + 1). Число q 0 (цифра единиц частного), удовлетворяющее последнему неравенству, можно найти подбором, воспользовавшись таблицей умножения. Получаем, что q 0 = 4 и, следовательно, неполное частное q = 90 + 4 = 94. Остаток находится вычитание: 378 – 4 × 94 = 2.
Итак, при делении числа 378 на 4 получается неполное частное 94 и остаток 2: 378 – 4 × 94 + 2.
Описанный процесс является основой деления уголком:
Аналогично выполняется деление многозначного числа на многозначное . Разделим, например, 4316 на 52. Выполнить это деление - значит найти такие целые неотрицательные числа q и r, что 4316 = 52 q + r , 0£ r < 52, а неполное частное должно удовлетворять неравенству 52 q £ 4316 < 52 (q+1).
Определим число цифр в частном q. Очевидно, частное заключено между числами 10 и 100 (т.е. q - двузначное число), так как 520 < 4316 < < 5200. Чтобы найти цифру десятков частного, умножим последовательно делитель 52 на 20, 30, 40, 50 и т.д. Поскольку 52 × 80 = 4160, а 52 × 90 = 4680 и 4160 < 4316 < 4680, то неполное частное заключено между числами 80 и 90, т.е. q = 80 + q 0 . Но тогда должны выполняться неравенства:
52× (80+ q 0) £ 4316 < 52 × (80+ q 0 + 1),
4160 + 52 q 0 £ 4316 < 4160 + 52× (q 0 + 1),
52 q 0 £ 156 < 52 × (q 0 + 1).
Число q 0 (цифру единиц частного), удовлетворяющее последнему неравенству, можно найти подбором: 156 = 52× 3, т.е. имеем случай, когда остаток равен 0. Следовательно, при делении 4316 на 52 получается частное 83.
Приведенные рассуждения лежат в основе деления уголком:
Конец работы -
Эта тема принадлежит разделу:
Непротиворечивая система аксиом называется независимой, если никакая из аксиом этой системы не является следствием других аксиом этой системы
При аксиоматическом построении теории по существу все утверж дения выводятся путем доказательства из аксиом Поэтому к системе аксиом предъявляются... Система аксиом называется непротиворечивой если из нее нельзя логически... Если система аксиом не обладает этим свойством она не может быть пригодной для обоснования научной теории...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Все темы данного раздела:
Количественные натуральные числа. Счет
Аксиоматическая теория описывает натуральное число как элемент бесконечного ряда, в котором числа располагаются в определенном порядке, существует первое число и т.д. Другими словами, в аксиоматик
Вопросы для самоконтроля
1. Назовите виды множеств, дайте им характеристику. Какие можно производить операции над множествами?
2. Что такое «число», «цифра», «счет»?
3. В чем связь и различие счета и изме
Теоретико-множественный смысл частного натуральных чисел.
Основная литература;
Дополнительная литература
Введение. Введя понятие отрезка натурального ряда, мы выяснил
Теоретико-множественный смысл суммы
Сложение целых неотрицательных чисел связано с объединением конечных непересекающихся множеств. Например, если множество А содержит 5 элементов, а множество В - 4 элемента и пересечен
Теоретико-множественный смысл разности
В аксиоматической теории вычитание натуральных чисел определено как операция, обратная сложению: а – b = с Û ($ сÎN) b + с = а.
Вычитание целых неотрицательных чисел определяет
Теоретико-множественный смысл произведения
Определение умножения натуральных чисел в аксиоматической теории основывается на понятии отношения «непосредственно следовать за» и сложении. В школьном курсе математики используется другое определ
Теоретико-множественный смысл частного натуральных чисел
В аксиоматической теории деление определяется как операция, обратная умножению, поэтому между делением и умножением устанавливается тесная взаимосвязь. Если а× b = с, то, зная произведение с
ТЕМА 14. ПОЗИЦИОННЫЕ И НЕПОЗИЦИОННЫЕ СИСТЕМЫ ИСЧИСЛЕНИЯ
Содержание
1. Позиционные и непозиционные системы счисления.
2. Запись числа в десятичной системе счисления.
Основная литература ;
Язык для наименования, записи чисел и выполнения действий над ними называют системой счисления.
Называть числа и вести счет люди научились еще до появления письменности. В этом им помогали, прежде всего, пальцы рук и ног. Издревле употреблялся еще такой вид инструментального счета, как деревя
Запись числа в десятичной системе счисления
Как известно, в десятичной системе счисления для записи чисел пользуется 10 знаков (цифр): 0, 1,2, 3, 4, 5, 6, 7, 8, 9. Из них образую конечные последовательности, которые являются краткими записям
Алгоритм сложения
Сложение однозначных чисел можно выполнить, основываясь на определении этого действия, но чтобы всякий раз не обращаться к определению, все суммы, которые получаются при сложении однозначных чисел,
Алгоритм вычитания
Вычитание однозначного числа b из однозначного или двузначного числа а, не превышающего 18, сводится к поиску такого числа с, что b + с = а, и происходит с учетом таблицы сложения однозначных чисел
Описанный процесс позволяет сформулировать в общем виде алгоритм вычитания чисел в десятичной системе счисления.
1. Записываем вычитаемое под уменьшаемым так, чтобы соответствующие разряды находились друг под другом.
2. Если цифра в разряде единиц вычитаемого не превосходит соответствующей цифры умен
Алгоритм умножения
Умножение однозначных чисел можно выполнить, основываясь на определении этого действия. Но чтобы всякий раз не обращаться к определению, все произведения однозначных чисел записывают в особую табли
Обобщением различных случаев деления целого неотрицательного числа а на натуральное число b является следующий алгоритм деления уголком.
1. Если а =b, то частное q = 1, остаток r = 0.
2. Если а >b и число разрядов в числах а и b одинаково, то частное q находим перебором, последовательно умножая b на 1, 2, 3, 4, 5, 6, 7,
Наименьшее общее кратное и наибольший общий делитель.
4. Простые числа.
5. Способы нахождения наибольшего общего делителя и наименьшего общего кратного чисел.
Основная литература ;
Дополнительн
Отношение делимости и его свойства
Определение.Пусть даны натуральные числа а и b. Говорят, что число а делится на число b, если существует такое натуральное число q, что а = bq.
В этом случае чис
Признаки делимости
Рассмотренные в свойства отношения делимости позволяют доказать известные признаки делимости чисел, записанных в десятичной системе счисления, на 2, 3, 4, 5, 9.
Признаки делимости позволя
Наименьшее общее кратное и наибольший общий делитель
Рассмотрим известные из школьного курса математики понятия наименьшего общего кратного и наибольшего общего делителя натуральных чисел, сформулируем их основные свойства, опустив все доказательства
Простые числа
Простые числа играют большую роль в математике - по существу они являются «кирпичами», из которых строятся составные числа.
Это утверждается в теореме, называемой основной теоремой арифмет
Способы нахождения наибольшего общего делителя и наименьшего общего кратного чисел
Рассмотрим сначала способ, основанный на разложении данных чисел на простые множители.
Пусть даны два числа 3600 и 288. Представим их в каноническом виде: 3600 = 24×3
ТЕМА 17. О РАСШИРЕНИИ МНОЖЕСТВА НАТУРАЛЬНЫХ ЧИСЕЛ
Содержание
1. Понятие дроби.
2. Положительные рациональные числа.
3. Запись положительных рациональных чисел в виде десятичных дробей.
4. Действительные ч
Понятие дроби
Пусть требуется измерить длину отрезка х с помощью единичного отрезка е (рис. 1). При измерении оказалос
Положительные рациональные числа
Отношение равенства является отношением эквивалентностинамножестве дробей, поэтому оно порождает на нем классы эквивалентности. В каждом таком классе содержатся равные междусобой дроби.
На
Сложение положительных рациональных чисел коммутативно и ассоциативно,
("а, b Î Q+) а + b= b + а;
("а, b, с Î Q+) (а + b)+ с = а + (b+ с)
Прежде чем сформулировать определе
Запись положительных рациональных чисел в виде десятичных дробей
Впрактической деятельности широко используются дроби, знаменатели которых являются степенями 10. Их называют десятичными.
Определение. Десят
Действительные числа
Одним из источников появления десятичных дробей является деление натуральных чисел, другим - измерение величин. Выясним, например, как могут получиться десятичные дроби при измерении длины отрезка.
Теоретико-множественный смысл разности.
8. Отношения «больше на» и «меньше на».
9. Правила вычитания числа из суммы и суммы из числа.
10. Из истории возникновения и развития способов записи натуральных чисел и нуля.
Множество положительных рациональных чисел как расширение множества натуральных чисел.
27. Запись положительных рациональных чисел в виде десятичных дробей.
28. Действительные числа.
МОДУЛЬ 4. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ВЕЛИЧ
Понятие положительной скалярной величины и ее измерения
Рассмотрим два высказывания, в которых используется слово «длина»:
1) Многие окружающие нас предметы имеют длину.
2) Стол имеет длину.
В первом предложении утверждается,
«Деление на однозначное число» - Алгоритм письменного деления. Деление «в столбик». Устный счёт. Найти первое неполное делимое. Самостоятельная работа. Найти цифры в каждом разряде частного. Деление на однозначное число «в столбик». Определить число цифр в частном.
«Задания на деление» - Сколько кг воздуха потребуется на наш класс. Экология. Скворец. Хозяева нашей природы. Заинька-трусишка. Дятел. Проверьте себя. Индюк. Поползень. Определи свое настроение. Гепард и зебра. Сколько видов растений на Земле на грани исчезновения. Деление на двузначное число. Наука. Трудолюбивые санитары леса.
«Деление на 9» - Вы готовы к волшебству. Умножение девяти и на 9, соответствующие случаи деления. Положите обе ладони на стол и запомните номера ваших пальчиков. Компьютер-математик готов работать с нами, А главное число узнаете сами. (Через 5 секунд фигуры удаляем с помощью кнопок вверх-вниз.). Цель урока. I. Организационный момент.
«Смысл действия деления» - Выбор этого подхода. Численность множеств, полученных в результате разбиения. Частное может обозначать число частей. Девочек две. Основа формирования. Число 5 означает, что 2 содержится в 10 пять раз. У Коли 10 тетрадей, у Пети – 2. Одни будут брать по одному яблоку. Множество всех яблок будет разделено.
«Математика 2 класс» - На сколько больше банок краски израсходовали, чем осталось? Станция «Узнавай-ка». Периметр квадрата со стороной 5см. Сумма множитель угол частное произведение единица вычитание. «Закрепляй-ка». Сколько банок краски осталось? «Неопознанные объекты». Узнайте периметр прямоугольника со сторонами 7см и 4см.
«Математика Деление» - Выполните деление. Число х Положительное Положительное Отрицательное Отрицательное. Проверь себя: Частное х и у. Число у Положительное Отрицательное Положительное Отрицательное. Какое число получится? Правила: Отрицательное. В каких случаях может быть верно равенство: Верно ли выполнено деление: Математика 6 класс.
Всего в теме 27 презентаций
В процессе изучения деления многозначных чисел учащиеся должны усвоить основные устные и письменные приёмы деления, овладеть соответствующими вычислительными умениями и навыками, расширить, углубить и систематизировать знания о действии деления, их свойстве, о взаимосвязях между результатами и компонентами действий, об изменении произведения и частного при изменении одного из компонентов.
Алгоритм письменного деления:
Образуют первое неполное делимое и устанавливают число цифр частного, неполное делимое делят на делитель, чтобы найти соответствующую цифру частного;
Найденную цифру частного умножают на делитель, для того чтобы узнать, сколько единиц соответствующего разряда разделили;
Полученное произведение вычитают из неполного делимого, для того чтобы узнать, сколько единиц этого разряда осталось разделить;
Проверяют, правильно ли найдена цифра частного, сравнив полученную разность с делителем.
При ознакомлении с приёмом письменного деления на однозначное число целесообразно сначала выполнить деление устно с развёрнутой записью и подробным объяснением. Так, предлагается решить пример 956:4. Ученики выделяют удобные слагаемые и выполняют деление:
956:4=(800+120+36) :4=800:4+120:4+36:4=200+30+9=239
При этом учитель объясняет, что решение этого примера можно выполнить письменно и записать его в столбик. Показывает запись и даёт такое объяснение:
Делимое 956, делитель 4. Первое неполное делимое-9сот., значит, в частном будет три цифры. Узнаем, сколько сотен будет в частном: разделим 9 на 4, получится 2. Узнаем, сколько сотен разделили: умножим 2 на 4, получится 8. Узнаем, сколько осталось разделить: вычтем 8 из 9, получится 1. Одну сотню нельзя разделить на 4 так, чтобы получить сотни, значит, цифра 2 найдена правильно.
Образуем второе неполное делимое: 1 сот.-это10 дес., к 10 дес. Прибавим 5 дес., получится 15 дес. Узнаем, сколько десятков будет в частном: разделим 15 на 4, получится 3 и т д. Частное 239.
Усвоению приёма письменного деления помогает использование памятки с заданиями, записанными на карточках или в виде плаката, выполнение которых в указанном порядке приводит к нахождению частного.
Задания памятки:
1. Прочитай и запиши пример.
2. Выдели первое неполное делимое и установи число цифр в частном.
3. Раздели неполное делимое на делитель и найди цифру частного.
4. Умножь цифру частного на делитель и узнай, сколько единиц этого разряда разделили.
5. Вычисли полученное произведение из неполного делимого и узнай, сколько единиц этого разряда осталось разделить.
6. Проверь, правильно ли подобрана цифра частного.
7. Образуй следующее неполное делимое и продолжай деление также до конца.
Рассматриваются не только случаи деления на однозначное число без остатка, но и с остатком. Рассуждение при делении с остатком ведётся также, как и при делении без остатка. В записи решения таких примеров остаток подписывается под последней чертой.
Деление на двузначные и трёхзначные разрядные числа. Подготовкой к введению новых приёмов деления будет повторение приёмов деления без остатка на 10, 100 и 1000, введение приёмов деления с остатком на эти числа, а также изучение свойства деления числа на произведение.
Пусть требуется разделить:
Первое неполное делимое-498 дес., значит, в частном будет 2 цифры. Узнаем, сколько десятков будет в частном: разделим 498 на 10 и полученное частное 49 разделим на 6, поучится 8. Узнаем сколько десятков разделили: умножим 60 на 8, получится 480. Узнаем, сколько десятков осталось разделить: вычтем 480 из 498, получится 18. Нельзя 18 десятков разделить на 60 так, чтобы получились десятки, значит, цифра десятков подобрана правильно. Образуем второе неполное делимое: 18 дес-это 180 ед.
При делении многозначных чисел на двузначное и трёхзначное число пользуются свойством деления суммы на число. Для нахождения цифр частного пользуются приёмом замены делителя разрядным числом.
Приознакомление с делением на двузначное число сначала решаются примеры на деление без остатка и с остатком трёхзначных чисел, когда цифру частного находят в результате одной пробы и когда в частном получают однозначное число. Здесь ученики знакомятся с приёмом замены делителя ближайшим разрядным числом. 315:63.
Чтобы найти цифру частного, заменим делитель ближайшим меньшим разрядным числом 60 и будем делить 315 на 60, для этого достаточно разделить 31 на 6, получим 5. Цифра 5 не окончательная а пробная, потому что надо было 315 делить на 63, а не на 60. Цифру 5 проверим: умножим 63 на 5 (устно), получим 315, значит, цифра 5 верна.
Опыт показывает, что при письменном делении на двузначное число целесообразнее в большинстве случаев заменять делитель ближайшим меньшим разрядным числом. При этом меньше изменений вносить в делитель: сохраняется число десятков, изменяется только число простых единиц.
Приём деления на трёхзначное число аналогичен приёму деления на двузначное. Например, при делении на 643 делитель заменяем числом 600 и цифры частного находим путём последовательного деления числа на 100 и на 6. Цифра частного проверяется устно, и в этом основная трудность деления. Можно объяснить детям, что при трёхзначном делителе нет надобности умножать на цифру частного всё трёхзначное число. Достаточно умножить только две цифры высших разрядов и сопоставить полученный результат с неполным делимым. Такого рода устные вычисления учащимся доступны.
Навыки письменного деления, особенно деления на двузначное и трёхзначное число, являются сложными. Поэтому, чтобы они успешно формировались, необходимо выполнить большое количество разнообразных упражнений в течении длительного времени.
Решение уравнений;
Сравнение числовых выражений;
Нахождение ошибок в вычислениях;
Выполнение письменных вычислений в решении текстовых задач;
©2015-2017 сайт
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Деление чисел рассматривают как действие деления с остатком: разделить целое неотрицательное число a на натуральное число b - это значит найти такие целые неотрицательные числа q и r , что a = b·q+ r , причем 0 ≤ r < b .
Если на однозначное число делят однозначное или двузначное (не превышающее 89), то используется таблица однозначных чисел. Например, частным чисел 56 и 8 будет число 7, так как 8·7 = 56. Если же надо разделить 52 на 8, то находят ближайшее к нему меньшее число, которое делится на 8 - это будет число 48, и, следовательно, неполным частным при делении 52 на 8 будет число 6. Чтобы найти остаток, надо из 52 вычесть 48: 52 - 48 = 4. Таким образом, 52 = 8·6 + 4, т.е. при делении 52 на 8 получается неполное частное 6 и остаток, равный 4.
Задача 8. Проиллюстрировать теоретические основы деления трехзначного числа 377 на однозначное число 4.
Решение . Разделить 377 на 4 - это значит найти такое неполное частное q и остаток r , что 377 = 4q + r , причем остаток r должен удовлетворять условию 0 ≤ r < b , а неполное частное q - условию 4 q ≤ 377 < 4·(q + 1).
Определим, сколько цифр будет содержаться в записи числа q . Однозначным число q быть не может, так как тогда произведение 4q может быть максимально равно 36 и, значит, не будут выполняться условия, сформулированные выше для r и q . Если число q двузначное, т.е. если 10 < q < 100, то тогда 40 < 4q < 400 и, следовательно, 40 < 377 < 400, что верно. Значит, частное чисел 377 и 4 - число двузначное.
Чтобы найти цифру десятков частного, умножим последовательно делитель 4 на 20, 30, 40 и т.д. Поскольку 4·90 = 360, а 4·100 = 400, и 360 < 377 < 400, то неполное частное заключено между числами 90 и 100, т.е. q = 90 + q0 . Но тогда должны выполняться неравенства:
4·(90 + q0 ) ≤ 377 < 360 + 4·(90 + q0 + 1), откуда
360 + 4q0 ≤ 377 < 360 + 4·(q0 + 1) и 4q 0 ≤ 17 < 4·(q0 + 1).
Число q0 (цифра единиц частного), удовлетворяющее последнему неравенству, можно найти подбором, воспользовавшись таблицей . Получаем, что q0 = 4 и, следовательно, неполное частное q = 90 + 4 = 94. Остаток находится вычитанием: 377 - 4·94 = 1.
Итак, при делении числа 377 на 4 получается неполное частное 94 и остаток 1: 377=4·94+1.
Задача 9. Проиллюстрировать теоретические основы деления многозначного числа 4316 на многозначное число 52.
Решение . Разделить 4316 на 52 - это значит найти такие целые неотрицательные числа q и r , что 4316 = 52 q + r , 0 ≤ r < 52, а неполное частное должно удовлетворять неравенству 52q ≤ 4316 < 52(q + 1).
Определим число цифр в частном q. Очевидно, частное заключено между числами 10 и 100 (т.е. q - двузначное число), так как 520 < 4316 < 5200. Чтобы найти цифру десятков частного, умножим последовательно делитель 52 на 20, 30, 40, 50 и т.д. Поскольку 52·80 = 4160, а 52·90 = 4680 и 4160 < 4316 < 4680, то неполное частное заключено между числами 80 и 90, т.е. q = 80 + q0. Но тогда должны выполняться неравенства:
52·(80 + q0 ) ≤ 4316 < 52·(80 + q0 + 1),
4160 + 52 q0 ≤ 4316 < 4160 + 52·(q0 + 1),
52 q0 ≤ 153 < 52·(q0 + 1).
Число q0 (цифру единиц частного), удовлетворяющее последнему неравенству, можно найти подбором: 156 = 52·3, т.е. имеем случай, когда остаток равен 0. Следовательно, при делении 4316 на 52 получается частное 83.
Приведенные рассуждения лежат в основе деления уголком:
Обобщением различных случаев деления целого неотрицательного числа а на натуральное число b является следующий алгоритм деления уголком.
1. Если а = b , то частное q = 1, остаток r = 0.
2. Если а > b и число разрядов в числах a и b одинаково, то частное q находим перебором, последовательно умножая b на 1, 2, 3, 4, 5, 6, 7, 8, 9, так как а < 10b . Этот перебор можно ускорить, выполнив деление с остатком цифр старших разрядов чисел а и b.
3. Если а > b и число разрядов в числе а больше, чем в числе b, то записываем делимое а и справа от него делитель b, который отделяем от а уголком и ведем поиск частного и остатка в такой последовательности:
а) выделяем в числе а столько старших разрядов, сколько разрядов в числе b или, если необходимо, на один разряд больше, но так, чтобы они образовывали число d1 больше или равное b. Перебором находим частное q1 чисел d1 и b, последовательно умножая b на 1, 2, 3, 4, 5, 6, 7, 8, 9. Записываем q1 под уголком (ниже b) ;
б) умножаем b на q1 и записываем произведение под числом а так, чтобы младший разряд числа bq1 был написан под младшим разрядом выделенного числа d1 ;
в) проводим черту под bq1 и находим разность r1 = d1 - bq1 ;
г) записываем разность r1 под числом bq1, приписываем справа к r1 старший разряд из неиспользованных разрядов делимого а и сравниваем полученное число d2 с числом b.
д) если полученное число d2 больше или равно b, то относительно него поступаем согласно п. 1 или п. 2. Частное q2 записываем после q1 ;
е) если полученное число d2 меньше b , то приписываем еще столько следующих разрядов, сколько необходимо, чтобы получить первое число d3, большее или равное b. В этом случае записываем после q1 такое же число нулей. Затем относительно d3 поступаем согласно пункты 1, 2. Частное q2 записываем после нулей. Если при использовании младшего разряда числа а окажется, что d3 < b, то тогда частное чисел d3 и b равно нулю, и этот нуль записывается последним разрядом к частному, а остаток r = d3.
Упражнения для самостоятельной работы
1. Не выполняя деления, определите число цифр частного чисел:
а) 475 и 7; б) 6134 и 226; в) 5683 и 25; г) 43127 и 536.
2. Проиллюстрируйте теоретические основы деления трехзначного числа 868 на однозначное число 3.
3. Найдите двумя способами значение выражения:
а) (297 + 405 + 567):27; в) 56·(378:14);
б) (240·23):48; г) 15120:(14·5·8).
4. Найдите значение выражения:
а) 8919:9 + 114240:21; б) 1190 - 35360: 34 + 271; в) 8631 - (99 + 44352:63);
г) 48600·(5045 - 2040) : 243 - (8604 3:43 + 504)·200.